最近在看《Python科学计算(第二版)》这本书,看到第五章后直接跳到了最后一章的实例部分,花了很久时间把第一个实例弄懂了七七八八,现在就来记录一下。
注:代码是书中的代码,不是本人所写,本文只是在详解代码。
泊松混合是一种图像合成算法,它将源图像中指定区域内的纹理信息复制到目标图像的对应区域内。
纹理信息通过拉普拉斯算子计算,可以直接通过OpenCV中的Laplacian()来计算。对于3x3的情况,Laplacian()实际上就是使用如下卷积核与图像进行卷积运算。
\[\begin{bmatrix} 0&1&0\\ 1&-4&1\\ 0&1&0 \end{bmatrix}\]即图像中每个像素值乘以-4后加上其上下左右4个像素的值。所谓泊松混合,就是指对于指定的区域,让目标图像的Laplacian运算结果与源图像的运算结果相同。
所谓泊松混合,就是指对于指定的区域,让目标图像的Laplacian运算结果与源图像的运算结果相同。
下图显示了泊松混合运算过程。从左侧开始:
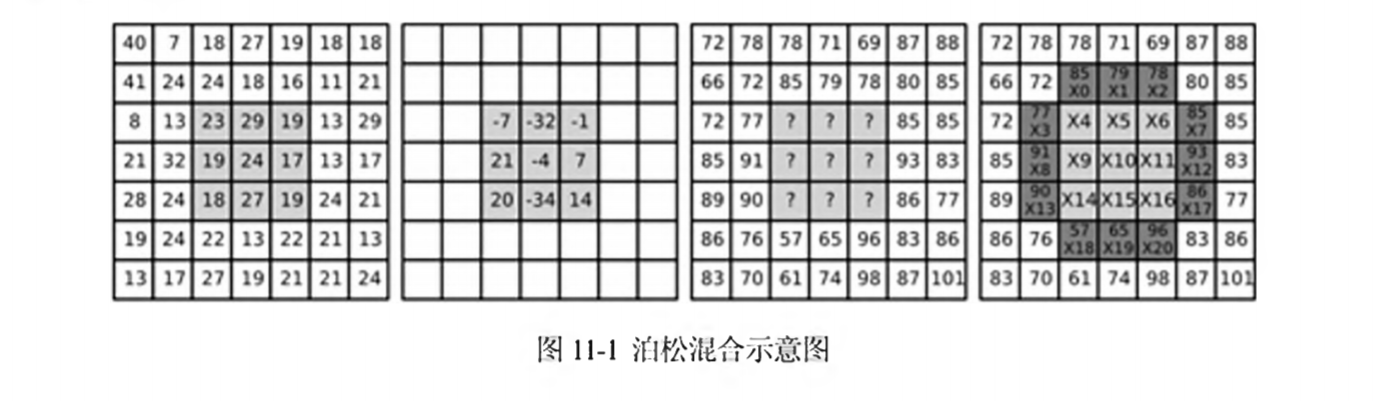
- 源图像:指定区域为浅灰色。
- 对源图像进行拉普拉斯运算的结果,(整个都需要计算,图中只显示了目标区域)
- 目标图像,其中用“?”表示未知值。这些未知值要保证对于指定的区域内,目标图像的拉普拉斯运算结果与源图像相同。
- 对目标图像中的未知值进行编号,以便生成方程组。
如果用未知数x0~x8表示9个未知的像素点,那么它们的值需要满足如下方程组:
\[-4*x0+85+77+x1+x3=-7\\ -4*x1+79+x0+x2+x4=-32\\ ...\\ -4*x8+86+96+x5+x7=14\\\]每个方程的右边的值就是每个未知像素对应的源图像的拉普拉斯运算值,而方程左边则是通过拉普拉斯卷积核展开的公式,每个未知像素的上下左右4个相邻的像素可能是已知的值或未知的像素。
因此计算泊松混合最终是求解这样一个方程组。由于涉及到的未知数太多,需要采用SciPy的稀疏矩阵运算相关函数:scipy.sparse.linalg.spsolve(),需要构造出A、b两个系数矩阵。
import numpy as np
from matplotlib import pyplot as plt
import cv2
offset_x, offset_y = -36, 42
src = cv2.imread("vinci_src.png", 1)
dst = cv2.imread("vinci_target.png", 1)
mask = cv2.imread("vinci_mask.png", 0)
src_mask = (mask > 128).astype(np.uint8) # 0-1像素
offset_x, offset_y是原始图像与目标图像之间目标区域的偏移量。
cv.imread()函数是读入图片,vinci_mask.png是掩膜图像,标识需要被混合的区域。(该函数的具体用法请看imread())
src_mask = (mask > 128).astype(np.uint8)是将像素的取值范围改为了0-1,原图片中像素>128的像素设为1,其他设为0。
src_y, src_x = np.where(src_mask) # 所有像素值非0的坐标
# 通过第二个参数ddepth指定结果数组的元素类型,CV_16S表示结果为一个16为的符号整数数组。
# 将src图像进行拉普拉斯计算,并且取mask标注的部分
src_laplacian = cv2.Laplacian(src, cv2.CV_16S, ksize=1)[src_y, src_x, :] #❷
第一行代码:在源图片上按照mask上标注的像素进行提取,即在mask上提取所有像素为1的位置坐标,并且存在src_y, src_x中。
第二行代码:在源图片上进行拉普拉斯计算,计算完成后将mask上标注的地方的像素值提取出来。
写到这个地方我就将所有图片都打印出来看了看:
plt.imshow(src)
plt.imshow(dst)
plt.imshow(mask)
plt.imshow(src_mask)
plt.imshow(src_laplacian)
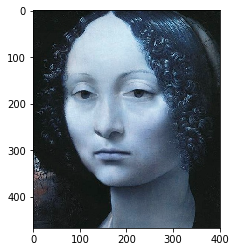

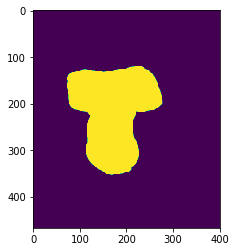


注:最后一张图片是源图片经过拉普拉斯计算出的图片,并没有切片操作。
dst_mask = np.zeros(dst.shape[:2], np.uint8) # 对dst构造一个标注数组初始化
dst_x, dst_y = src_x + offset_x, src_y + offset_y # 加上偏移量
dst_mask[dst_y, dst_x] = 1 #❶ 将对应需要标注的地方全部设为1
plt.imshow(dst_mask) # dst的mask已经构造完成
对目标图片初始化一个mask掩膜图片,和dst目标图片的长宽一样,但是它是一个二维图片。
由于源图片与目标图片有一定差异,因此会有一定偏移量,由源图片的标注位置加上偏移量即可得到目标图片的标注位置的坐标。
利用刚刚得到的目标图片中的标注像素坐标,将掩膜数组中对应位置的像素设置为1,这样目标图片的掩膜图片就制作好了。
最后一行代码是查看新做好的目标图片的掩膜图像。
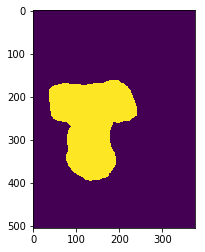
kernel = np.array([[0,1,0],[1,1,1],[0,1,0]], dtype=np.uint8) # 构造计算的核,单纯一个数组
# 函数可以对输入图像用特定结构元素进行膨胀操作, 该结构元素确定膨胀操作过程中的邻域的形状,
# 各点像素值将被替换为对应邻域上的最大值
dst_mask2 = cv2.dilate(dst_mask, kernel=kernel) #❷
plt.imshow(dst_mask2)
kernel是后面图片进行膨胀计算的核,值为一个矩阵:
\[\begin{bmatrix} 0&1&0\\ 1&1&1\\ 0&1&0 \end{bmatrix}\]cv2.dilate()是一个将图片进行膨胀计算的函数,在这个核的作用下,该膨胀计算大致实现的效果为,每个非零像素点的上下左右的像素点设置为和该像素点一样的值。则最终的效果就是整个图像会大一圈,但是由于一个像素太小,几乎看不出来。

dst_y2, dst_x2 = np.where(dst_mask2) #❸ 记录下标注像素的下标
dst_ye, dst_xe = np.where(dst_mask2 - dst_mask) #❹ 标注的边缘像素的坐标
variable_count = len(dst_x2) # 膨胀的标注像素的总个数
variable_index = np.arange(variable_count) #❶ 生成每个像素的下标序列
variables = np.zeros(dst.shape[:2], np.int) # 生成与dst同长宽的全零矩阵
variables[dst_y2, dst_x2] = variable_index # 将每个像素进行标注序号
第一行显示将膨胀后的目标掩膜图像的非零像素的坐标记录下来。
第二行代码用膨胀的目标像素矩阵减去了目标像素矩阵,因此就剩下了膨胀的一圈,也就是标注区域的边缘,并且将坐标记录下来。
第三行代码是计算了膨胀的目标标注像素的总个数。
第四行代码是生成了一个和膨胀目标标注像素个数相同长度的序列。
第五行代码生成一个与dst同长宽的全零矩阵。
第六行代码就是将所有非零像素按顺序把刚刚生成的序列赋值在相应的位置。得到的variables矩阵所有标注的点就是从0到len(dst_x2)-1的数。
x0 = variables[dst_y , dst_x ] #❷
x1 = variables[dst_y-1, dst_x ]
x2 = variables[dst_y+1, dst_x ]
x3 = variables[dst_y , dst_x-1]
x4 = variables[dst_y , dst_x+1]
x_edge = variables[dst_ye, dst_xe] #❸ 已知的像素值
此处的x0, x1, x2, x3, x4分别对应着中间像素、上下左右像素,存储着在该像素位置的序列。
x_edge则是之前利用膨胀生成的边缘像素。
from scipy.sparse import coo_matrix
inner_count = len(x0) # 原本的标注个数
edge_count = len(x_edge) # 边缘的个数
r = np.r_[x0, x0, x0, x0, x0, x_edge]
c = np.r_[x0, x1, x2, x3, x4, x_edge]
v = np.ones(inner_count*5 + edge_count) # 生成和r、c等大小的全1向量
v[:inner_count] = -4 # 前inner_count乘-4,中心点*-4
A = coo_matrix((v, (r, c))).tocsc() # 线性方程组中各个未知数的系数矩阵A
inner_count、edge_count分别存储着dst原始的标注区域像素个数和边缘的像素个数。
由于计算泊松混合最终是求解一个方程组,未知数的个数就是区域中标注的像素的个数,又为了便于生成系数矩阵A,边缘的像素也被设置为未知数,后续直接给这些像素点赋值。
为了生成系数矩阵A,我们需要生成一个未知数*未知数大小的矩阵,行索引就是[x0, x0, x0, x0, x0, x_edge];列索引为[x0, x1, x2, x3, x4, x_edge];系数向量为V,前inner_count个数字为-4,后面皆为1,inner为x0的长度,前inner_count的像素都为x0即中心像素,根据一开始给出的矩阵核可知,中心像素的系数为-4,上下左右的像素系数为1。
生成了行列索引以及对应位置的系数后利用coo_matrix().tocsc()方法形成一个稀疏矩阵,此时稀疏矩阵A就做好了。
from scipy.sparse.linalg import spsolve
order = np.argsort(np.r_[variables[dst_y, dst_x], variables[dst_ye, dst_xe]]) #❶
result = dst.copy()
for ch in (0, 1, 2): #❷
b = np.r_[src_laplacian[:,ch], dst[dst_ye, dst_xe, ch]] #❸
u = spsolve(A, b[order]) #❹
u = np.clip(u, 0, 255)
result[dst_y2, dst_x2, ch] = u #❺
首先将目标掩膜图像的标注像素以及边缘像素进行排序,返回排序后的坐标。为了和A矩阵进行匹配则需要进行排序。
接着对dst进行拷贝。
对于图像的三个通道分别进行计算,则用了一个for循环:
先形成b向量,即源图片的拉普拉斯计算结果中对应通道上标注的所有的值,以及目标图片上边缘像素对应通道的值。
对于为什么所有的图片上都把边缘像素的值带上是因为,我们一开始为了更方便的构造矩阵A,从而将边缘像素(已知)也设置为了未知数,后面在b向量的对应位置上把边缘像素的真实值写上相当于在后面的方程组上定义了边缘像素的值:
\[x0=85\\ x1=79\\ x2=78\\ ...\]其中x0、x1…为边缘像素对应的未知数。
接下来有了系数矩阵A以及偏移量向量b,就可以利用scipy中的spsolve()函数进行求解,得到u,再将u的值范围扩展到0~255;最后在result数组上将目标图片上被掩膜图标注的像素全部进行替换即可。注意每个通道都要进行一次这样的计算与新值替换。最终泊松混合合成图像就大功告成了!!
最后来看看效果图片吧!
fig, axes = plt.subplots(1, 4, figsize=(10, 4))
ax1, ax2, ax3, ax4 = axes.ravel()
ax1.imshow(src[:, :, ::-1])
ax2.imshow(mask, cmap="gray")
ax3.imshow(dst[:, :, ::-1])
ax4.imshow(result[:, :, ::-1])
for ax in axes.ravel():
ax.axis("off")
fig.subplots_adjust(wspace=0.05)

全部代码如下(其中多处有我自己写的注释,但是再强调一遍,这个代码不是我写的,我只是进行全部详尽的解释):
# -*- coding: utf-8 -*-
"""
Created on Thu Aug 15 09:31:34 2019
@author: 86153
"""
import numpy as np
from matplotlib import pyplot as plt
import cv2
offset_x, offset_y = -36, 42
src = cv2.imread("vinci_src.png", 1)
dst = cv2.imread("vinci_target.png", 1)
mask = cv2.imread("vinci_mask.png", 0)
src_mask = (mask > 128).astype(np.uint8) # 0-1像素
src_y, src_x = np.where(src_mask) #❶ 所有像素值非0的坐标
# 通过第二个参数ddepth指定结果数组的元素类型,CV_16S表示结果为一个16为的符号整数数组。
# 将src图像进行拉普拉斯计算,并且取mask标注的部分
src_laplacian = cv2.Laplacian(src, cv2.CV_16S, ksize=1)[src_y, src_x, :] #❷
plt.imshow(src)
plt.imshow(dst)
plt.imshow(mask)
plt.imshow(src_mask)
plt.imshow(src_laplacian)
dst_mask = np.zeros(dst.shape[:2], np.uint8) # 对dst构造一个标注数组初始化
dst_x, dst_y = src_x + offset_x, src_y + offset_y # 加上偏移量
dst_mask[dst_y, dst_x] = 1 #❶ 将对应需要标注的地方全部设为1
plt.imshow(dst_mask) # dst的mask已经构造完成
kernel = np.array([[0,1,0],[1,1,1],[0,1,0]], dtype=np.uint8) # 构造计算的核,单纯一个数组
# 函数可以对输入图像用特定结构元素进行膨胀操作, 该结构元素确定膨胀操作过程中的邻域的形状,
# 各点像素值将被替换为对应邻域上的最大值
dst_mask2 = cv2.dilate(dst_mask, kernel=kernel) #❷
plt.imshow(dst_mask2)
dst_y2, dst_x2 = np.where(dst_mask2) #❸ 记录下标注像素的下标
dst_ye, dst_xe = np.where(dst_mask2 - dst_mask) #❹ 标注的边缘像素的坐标
variable_count = len(dst_x2) # 膨胀的标注像素的总个数
variable_index = np.arange(variable_count) #❶ 生成每个像素的下标序列
variables = np.zeros(dst.shape[:2], np.int) # 生成与dst同长宽的全零矩阵
variables[dst_y2, dst_x2] = variable_index # 将每个像素进行标注序号
x0 = variables[dst_y , dst_x ] #❷
x1 = variables[dst_y-1, dst_x ]
x2 = variables[dst_y+1, dst_x ]
x3 = variables[dst_y , dst_x-1]
x4 = variables[dst_y , dst_x+1]
x_edge = variables[dst_ye, dst_xe] #❸ 已知的像素值
from scipy.sparse import coo_matrix
inner_count = len(x0) # 原本的标注个数
edge_count = len(x_edge) # 边缘的个数
r = np.r_[x0, x0, x0, x0, x0, x_edge]
c = np.r_[x0, x1, x2, x3, x4, x_edge]
v = np.ones(inner_count*5 + edge_count) # 生成和r、c等大小的全1向量
v[:inner_count] = -4 # 前inner_count乘-4,中心点*-4
A = coo_matrix((v, (r, c))).tocsc() # 线性方程组中各个未知数的系数矩阵A
from scipy.sparse.linalg import spsolve
order = np.argsort(np.r_[variables[dst_y, dst_x], variables[dst_ye, dst_xe]]) #❶
result = dst.copy()
for ch in (0, 1, 2): #❷
b = np.r_[src_laplacian[:,ch], dst[dst_ye, dst_xe, ch]] #❸
u = spsolve(A, b[order]) #❹
u = np.clip(u, 0, 255)
result[dst_y2, dst_x2, ch] = u #❺
#%fig=使用泊松混合算法将吉内薇拉·班琪肖像中的眼睛和鼻子部分复制到蒙娜丽莎的肖像之上
fig, axes = plt.subplots(1, 4, figsize=(10, 4))
ax1, ax2, ax3, ax4 = axes.ravel()
ax1.imshow(src[:, :, ::-1])
ax2.imshow(mask, cmap="gray")
ax3.imshow(dst[:, :, ::-1])
ax4.imshow(result[:, :, ::-1])
for ax in axes.ravel():
ax.axis("off")
fig.subplots_adjust(wspace=0.05)
最后想说一下这个图片排版问题,我不知道怎么把多个图片放在一行上,我查了很多方法,在我这里就不管用了,有点无奈,只能这样了,所以这次排版有些丑。
可能是我底子薄吧,这个代码看了很久,我几乎没有接触过图像处理的案例,也没有写过关于图像处理的代码,确实费了一些时间来看这个代码,尽管这个代码很简单。还是希望大家能多多支持~