《Python科学计算(第二版)》第11章第二个实例
最近在看《Python科学计算(第二版)》这本书,看到第五章后直接跳到了最后一章的实例部分,昨天刚刚看完第一个实例,虽然简单但是还是花了不少时间与精力,今天开始琢磨第二个实例,现在就来记录一下。
注:代码是书中的代码,不是本人所写,本文只是在详解代码。
这一个实例以悬链线、最速降线和单摆为例介绍如何使用SciPy中的integrate和optimize库模拟简单的经典力学现象。
悬链线
将绳子的两端固定在同一水平高度,绳子因重力作用而垂下所形成的形状被称为悬链线,它的曲线函数为:
\[\begin{equation} y=acosh(\frac{x}{a}) \end{equation}\]其中a为决定下垂程度的系数。
import pylab as pl
import numpy as np
from scipy import integrate
from scipy import optimize
import sympy
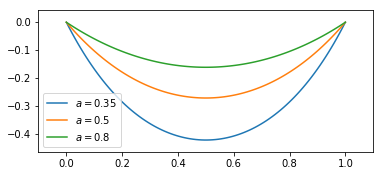
#%fig=各种长度的悬链线
def catenary(x, a):
return a*np.cosh((x - 0.5)/a) - a*np.cosh((-0.5)/a)
x = np.linspace(0, 1, 100)
for a in [0.35, 0.5, 0.8]:
pl.plot(x, catenary(x, a), label="$a={:g}$".format(a))
ax = pl.gca()
ax.set_aspect("equal")
ax.legend(loc="best")
pl.margins(0.1)
该部分代码中定义了函数catenary(x, a),该函数是悬链线的形状方程,但是经过了一定的平移,现经过(0, 0)和(1, 0)两个点,因此平移后的方程为$y=acosh(\frac{x-0.5}{a})-acosh(\frac{-0.5}{a})$。
x在0~1的范围内取了100个点,接着下垂系数a分别取了0.35、0.5、0.8三个数,进行计算对应的y值。
pl.gca()为获取当前的子图,接下来对图标进行属性设置;ax.set_aspect("equal")表示使得x轴每个单位长度和y轴的每个单位长度相同;ax.legend(loc="best")则是设置图例位置;pl.margins(0.1)修改图表的内边距。整个图就完成了,可以看下输出图效果:
接下来可以计算曲线长度,而曲线的长度可由如下公式进行计算:
\[\begin{equation} s=\int_0^1\sqrt{1+(\frac{dy}{dx})^2}dx \end{equation}\]下面代码是根据catenary()函数进行计算:
y = catenary(x, 0.35)
np.sqrt(np.diff(x)**2 + np.diff(y)**2).sum()
[out]
1.3765522648842718
上述代码先根据x的取值计算出了对应的y值,这时就等同于已知了一串在该函数上的点,再根据欧式距离公式计算相邻两点之间的距离,将这些距离累加可近似为曲线长度。
得到结果:1.3765522648842718
from sympy import symbols, cosh, S, sqrt, lambdify
#import sympy
x, a = symbols("x, a")
y = a * cosh((x - S(1)/2) / a)
s = sqrt(1 + y.diff(x)**2)
fs = lambdify((x, a), s, modules="math")
def catenary_length(a):
return integrate.quad(lambda x:fs(x, a), 0, 1)[0]
length = catenary_length(0.35)
length
[out]
1.3765789965047124
该代码主要是利用了sympy库进行符号运算。
首先定义了两个符号变量,x,a;
接下来给y定义了一个包含x、a的式子:$y=acosh(\frac{x-0.5}{a})$;
接着对于公式(2)中被积分的函数$\sqrt{1+(\frac{dy}{dx})^2}dx$进行了定义并且赋值为s;
又自定义一个表达式fs,函数lambdify()类似于lambda函数,可以进行函数定义,输入的是变量x、a,计算的函数为s;
最后定义了一个计算长度的函数catenary_length(),用函数integrate.quad()对上一行定义的fs进行0~1积分求解,并且取其中第0个数作为最终结果返回,这样利用积分计算曲线准确长度的代码就写好了。并且当a为0.35时的结果为1.3765789965047124,该结果与上个近似曲线长度的结果很是相似。
1.使用运动方程模拟悬链线
为了使用牛顿力学中的运动方程模拟悬链线,我们可以把悬链看成有多个由弹簧连接的质点系统,每个质点受到重力以及左右两个弹簧力。当质点运动时,它还会受到大小与速度成正比的阻力。为了使悬链两端的质点保持静止,可以不计算其受力,因此这两个质点的加速度始终为0。每个质点有X与Y方向上的速度与加速度共4个状态,对于由N个质点构成的系统,共有4xN个状态。
#%fig=使用运动方程模拟悬链线,由于弹簧会被拉伸,因此悬链线略比原始长度长
N = 31
dump = 0.2 #阻尼系数
k = 100.0 #弹簧系数
l = length / (N - 1) #弹簧原长度
g = 0.01 #重力加速度
x0 = np.linspace(0, 1, N)
y0 = np.zeros_like(x0)
vx0 = np.zeros_like(x0)
vy0 = np.zeros_like(x0)
def diff_status(status, t):
x, y, vx, vy = status.reshape(4, -1)
dvx = np.zeros_like(x)
dvy = np.zeros_like(x)
dx = vx
dy = vy
s = np.s_[1:-1]
l1 = np.sqrt((x[s] - x[:-2])**2 + (y[s] - y[:-2])**2)
l2 = np.sqrt((x[s] - x[2:])**2 + (y[s] - y[2:])**2)
dl1 = (l1 - l) / l1
dl2 = (l2 - l) / l2
dvx[s] = -vx[s] * dump - (x[s] - x[:-2]) * k * dl1 - (x[s] - x[2:]) * k * dl2
dvy[s] = -vy[s] * dump - (y[s] - y[:-2]) * k * dl1 - (y[s] - y[2:]) * k * dl2 + g
return np.r_[dx, dy, dvx, dvy]
status0 = np.r_[x0, y0, vx0, vy0]
t = np.linspace(0, 50, 100)
r = integrate.odeint(diff_status, status0, t)
x, y, vx, vy = r[-1].reshape(4, -1)
r, e = optimize.curve_fit(catenary, x, -y, [1])
print("a =", r[0], "length =", catenary_length(r[0]))
x2 = np.linspace(0, 1, 100)
pl.plot(x2, catenary(x2, 0.35))
pl.plot(x2, catenary(x2, r))
pl.plot(x, -y, "o")
pl.margins(0.1)
首先,整个系统包含的质点总数N为31个,阻尼系数dump被设置为0.2,弹簧系数k设置为100,弹簧的初始长度为length/(N-1)(其中length已经在上个代码中求解出来了),重力加速度g设置为0.01;
设置好了各个常量后,开始定义系统中每个质点的4个状态:x0、y0、vx0、vy0,分别代表着在X与Y方向上的位置与速度共4个状态;其中x0取了0~1之间的N个点,代表各个质点的X方向上的坐标,同时初始化了其他三个状态量的向量。
我们一开始提到过每个质点的状态应是X与Y方向上的速度与加速度,然而对位置坐标求导则是速度,对速度求导则是加速度,现在我们则需要定义一个函数对刚刚定义的状态向量进行整体求导,从而得到我们所需要的状态量。
在diff_status()函数中,将参数中的status包含的四个状态向量分别赋值给x、y、vx、vy;对于各个变量的导数结果也初始化一下,得到dvx、dvy、dx、dy;对x,y的求导就是速度,因此直接将vx、vy的值赋值给dx、dy就好。
s = np.s_[1:-1]这一句代码定义了一个切片:去掉第一个数和最后一个数。
l1是前N-1条线段的l2范数(欧式距离),l2则是后N-1条线段的l2范数;对长度进行求导得到dl1、dl2;后面两行主要计算加速度也就是速度的导数,但是公式没有看懂,物理还没有学过这部分的知识,实在是讲解不了。
计算好了四种状态就按行连接并且返回结果,此时这个函数也就定义好了。
status0拼接了一开初始化的x0、y0、vx0、xy0;
接下来是求解常微分方程,而刚刚构造的diff_status()正式为了求解
常微分方程解完之后用optimize.curve_fit()函数对x,y进行拟合曲线;最后画图即可。
图如下所示:
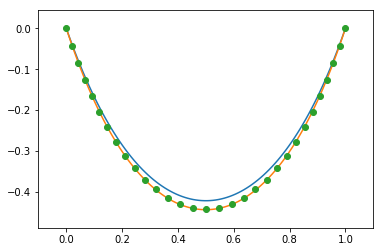
在图中圆点表示各个质点的最终位置,红色曲线为使用悬链线方程对质点位置进行拟合后得到的最佳拟合悬链线,而蓝色曲线为弹簧保持原长时的悬链线。为了使得最终状态接近原长时的悬链线,需要尽量大的弹簧系数和尽量小的重力加速度,这样能保证每根弹簧接近原长。
2.通过能量最小值计算悬链线
当质点之间为刚性连接时,弹簧不存储任何弹性势能,重力使得整个系统的重力只能降为最低,因此可以通过最小化势能计算各个质点的最终状态。由于悬链线的两端固定,而质点之间的距离固定,因此该最小化问题带有许多约束条件。为了尽量减少约束条件,我们以每个连接杆的角度为变量表示整条悬链线的状态。悬链线的一端固定在(0, 0)处。因此满足如下两个约束条件,其中$\theta_i$为每根杆的方向,l为杆的长度:
\[\begin{equation} \sum{lcos\theta_i}=1,\\ \sum{lsin\theta_i}=0 \end{equation}\]第i个质点的Y轴位置为:
\[\begin{equation} y_i=\sum_{k=0}^{i}lsin\theta_k \end{equation}\]势能P用下式表示:
\[\begin{equation} P=\sum{y_i} \end{equation}\]因此最小化问题就是找到一组$\theta_i$,它们满足两个约束条件,并且使得P最小,\theta_i的取值范围为$\frac{-\pi}{2}<\theta_i<\frac{\pi}{2}$。这种带等式约束条件的最小化问题可以使用scipy.optimize.fmin_slsqp()进行求解。
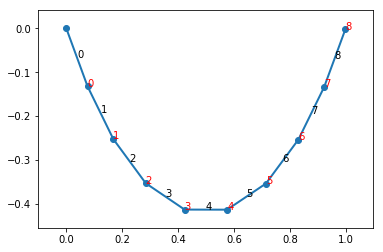
整个系统如下所示:
N = 30
l = length / N
def g1(theta):
return np.sum(l * np.cos(theta)) - 1.0
def g2(theta):
return np.sum(l * np.sin(theta)) - 0.0
def P(theta):
y = l * np.sin(theta)
cy = np.cumsum(y)
return np.sum(cy)
theta0 = np.arccos(1.0 / length)
theta_init = [-theta0] * (N // 2) + [theta0] * (N // 2) #❶
theta = optimize.fmin_slsqp(P, theta_init,
eqcons=[g1, g2], #❷
bounds=[(-np.pi/2, np.pi/2)]*N) #❸
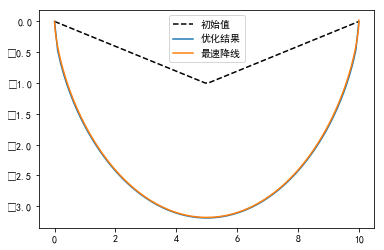
#%fig=使用fmin_slsqp()计算能量最低的状态,叉点表示最优化的初始状态
x_init = np.r_[0, np.cumsum(l * np.cos(theta_init))]
y_init = np.r_[0, np.cumsum(l * np.sin(theta_init))]
x = np.r_[0, np.cumsum(l * np.cos(theta))]
y = np.r_[0, np.cumsum(l * np.sin(theta))]
x2 = np.linspace(0, 1, 100)
pl.plot(x2, catenary(x2, 0.35))
pl.plot(x, y, "o")
pl.plot(x_init, y_init, "x")
pl.margins(0.1)
[out]
Optimization terminated successfully. (Exit mode 0)
Current function value: -7.765299463885223
Iterations: 9
Function evaluations: 288
Gradient evaluations: 9
首先定义了系统中质点的数量N为30,以及每条线段的长度l;
$\theta_i$角度乃为线段与向西方向的水平线之间的夹角。
后面的g1()函数计算最右端点的横坐标需要的条件:$\sum{lcos\theta_i}=1$;
g2()函数则是纵坐标需要满足的条件:$\sum{lsin\theta_i}=0$;
函数P()则是计算重力势能的函数,函数内的y表示的是每条线段对应在纵轴方向的长度;cy是对y的累加,由于y表示的单条线段的高度,而势能则是高度的累加;最后将势能cy求和就是系统的总体势能。
theta0是对每条线段的角度的初始化,为了提高优化的速度,则让初始值满足两个约束条件,如后图中的叉点所示。
fmin_slsqp()的eqcons参数是计算等式约束条件的函数列表。bounds参数是每个变量的取值范围列表。此外,如果最小化问题中存在不等式约束条件,可以通过ieqcons参数指定。当约束条件很多时,为了减少函数的调用参数,可以使用f_eqcons和f_ieqcons参数指定一个计算约束条件的函数,这两个函数返回的数组表示各个约束条件。
最终得到的图如下所示:
最速降线
所谓最速降线问题,是指在两点之间建立一条无摩擦的轨道,使得小球从高点到低点所需的时间最短。考虑两点高度相同的极端情况,显然这条曲线不是直线。根据维基百科的相关介绍,下降高度为D的最速降线满足如下方程:
\[\begin{equation} dx=\sqrt{\frac{y}{D-y}}dy \end{equation}\]由公式可知,y的取值范围为0到D之间。当D为1时,最速降线重点X轴坐标:
x, _ = integrate.quad(lambda y:np.sqrt(y/(1.0-y)), 0, 1)
print(x)
[out]
1.5707963267949878
可以得到曲线终点和起点之间X轴的差为$\frac{\pi}{2}$。
1.使用odeint()计算最速降线
使用odeint()对下面的微分方程进行积分即可得到最速降线的曲线:
程序如下所示:
#%fig=使用odeint()计算最速降线
def brachistochrone_curve(D, N=1000):
eps = 1e-8
def f(y, x):
y = min(max(eps, y), D) #❶
flag = -1 if x >= D * np.pi / 2 else 1 #❷
return flag * ((D - y) / y) ** 0.5
x0 = np.linspace(0, D * np.pi, N)
y = integrate.odeint(f, 0, x0)
return x0, y.ravel()
x, y = brachistochrone_curve(2.0)
pl.plot(x, -y);
当y=0时,曲线的切线为垂直方向,dy/dx无穷大,因此限制y的值必须大于极小值eps并小于D,这样才能保证积分正常进行。
由于使用微分方程计算的曲线只是左半边的曲线,完整的曲线相对于$x=D\pi/2$对称。为了odeint()能够计算完整的曲线,需要根据x的值判断$\frac{dy}{dx}$的符号。因此flag这一行代码则是进行符号的判断,最后将得到的结果乘以flag则为真正的值。
最后利用integrate.odeint()函数将定义的常微分方程f进行求解得到y。最终得到的结果如下所示:

2.使用优化算法计算最速降线
可以使用优化算法近似计算最速降线。首先将X轴从0到target等分为N-1份,每个点对应的Y轴坐标y就是要优化的自变量。优化的目标是计算小球经过该曲线所需的时间。根据能量守恒定理,可以计算出小球到达每个坐标点时的速度为$v=\sqrt{2gy}$。
小球经过每条线段的速度按照两个端点速度的平均值计算,线段的长度根据两个端点的距离计算,由此可以得出小球经过每条线段的时间。优化的目标就是所有这些时间之和的最小,即小球通过整条曲线的时间最短。
程序如下所示:
N = 100.0
target = 10.0
x = np.linspace(0, target, N)
tmp = np.linspace(0, -1, N // 2)
y0 = np.r_[tmp, tmp[::-1]]
g = 9.8
def total_time(y):
s = np.hypot(np.diff(x), np.diff(y)) #❶
v = np.sqrt(2 * g * np.abs(y)) #❷
avg_v = np.maximum((v[1:] + v[:-1])*0.5, 1e-10) #❸
t = s / avg_v
return t.sum()
def fix_two_ends(y):
return y[[0, -1]]
y_opt = optimize.fmin_slsqp(total_time, y0, eqcons=[fix_two_ends]) #❹
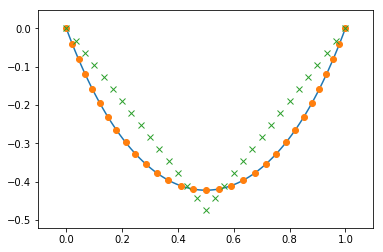
pl.plot(x, y0, "k--", label=u"初始值")
pl.plot(x, y_opt, label=u"优化结果")
x2, y2 = brachistochrone_curve(target / np.pi)
pl.plot(x2, -y2, label=u"最速降线")
pl.legend(loc="best");
从0~10之间等分100份,得到等分后的各点的横坐标x,对于高度y值初始化的是由0~1之间等分N//2之后的值(进行了一次倒序),后又定义了重力加速度g为9.8。
接下来定义了需要被优化的函数: total_time();hypot()函数返回欧几里德范数,即每条线段的长度;v则是利用能量守恒公式计算小球到达每点的速度;avg_v计算每个线段的平均速度,为了防止平均速度为0导致无法计算时间,这里使用函数maximum()将速度的下限设置为$10^{-10}$;t则是用每条线段的长度除以对应线段上的平均速度得到通过该段线段的时间;最后返回时间t的总和,即为小球通过所有线段的时间。
函数fix_two_ends()返回首尾两点的高度y。
由于需要保证曲线两个端点的Y轴坐标为0,因此我们使用fmin_slsqp()优化函数,并用fix_two_ends()保证两个端点的Y轴坐标始终为0。最后得到最终结果如下图所示:
单摆模拟
如图所示,有一根不可伸长、质量不计的绳子,上端固定,下端系一质点,这样的装置叫作单摆:
根据牛顿力学定律,可以列出如下微分方程:
\[\begin{equation} \frac{d^2\theta}{dt^2}+\frac{g}{l}sin\theta=0 \end{equation}\]其中$\theta$为单摆的摆角,$l$为单摆的长度,$g$为重力加速度。次微分方程的符号解无法直接求出,因此只能调用odeint()对其求数值解。
odint()要求每个微分方程只包含一阶导数,因此我们需要对上面的微分方程做如下变形:
下面是利用odint()计算单摆轨迹的程序,以及摆角和时间的关系:
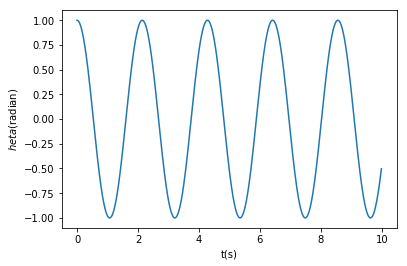
#%fig=初始角度为1弧度的单摆摆动角度和时间的关系
from math import sin
g = 9.8
def pendulum_equations(w, t, l):
th, v = w
dth = v
dv = - g / l * sin(th)
return dth, dv
t = np.arange(0, 10, 0.01)
track = integrate.odeint(pendulum_equations, (1.0, 0), t, args=(1.0,))
pl.plot(t, track[:, 0])
pl.xlabel(u"时间(秒)")
pl.ylabel(u"振动角度(弧度)");
重力加速度g设置为9.8;
pendulum_equations()函数是对公式(9)的实现,分别计算了角度$\theta$对时间$t$的导数,以及速度$v$对时间$t$的导数;
接下来利用integrate.odeint()求解常微分方程,得到track后进行画图,图如下所示:
1.小角度时的摆动周期
当最大摆动角度很小时,单摆的摆动周期可以使用如下公式计算:
\[\begin{equation} T_0=2\pi\sqrt{\frac{l}{g}} \end{equation}\]这是因为当$0«1$时,$sin\theta\approx\theta$,这样微分方程就变成了:
\[\begin{equation} \frac{d^2\theta}{dt^2}+\frac{g}{l}\theta=0 \end{equation}\]此微分方程的解是一个简谐振动方程,很容易计算其摆动周期。下面用SymPy对这个微分方程进行符号求解:
from sympy import symbols, Function, dsolve
t, g, l = symbols("t,g,l", positive=True) # 分别表示时间、重力加速度和长度
y = Function("y") # 摆角函数用y(t)表示
dsolve(y(t).diff(t,2) + g/l*y(t), y(t))
[out]
Eq(y(t), C1*sin(sqrt(g)*t/sqrt(l)) + C2*cos(sqrt(g)*t/sqrt(l)))
首先定义了变量t、g、l,以及函数y;接着用SymPy求解公式(11)的解。
由结果可知,简谐振动方程的解是由两个频率相同的三角函数构成的周期为$2\pi\sqrt{\frac{l}{g}}$。
2.大角度时的摆动周期
当初始角度增大时,会有无法忽略的误差,可用数值计算的方法求出单摆在任意初始摆角时的摆动周期。
g = 9.8
def pendulum_th(t, l, th0):
track = integrate.odeint(pendulum_equations, (th0, 0), [0, t], args=(l,))
return track[-1, 0]
要计算摆动周期,只需要计算从最大摆角到0摆角所需的时间摆动周期是此时间的4倍。为了计算出这个时间值,首先需要定义函数pendudlum_th()来计算长度$l$、初始角度为$th0$的单摆在时刻$t$的摆角:
该函数仍旧是使用integrate.odeint()函数进行常微分方程求解,其中t并非为一个值,而是一个序列。
接下来需要找到第一个使pendulum_th()的结果为0的时间即可。这相当于对pendulum_th()求解,可以使用scipy.optimize.fsolve()对这种非线性方程进行求解。
from scipy.optimize import fsolve
def pendulum_period(l, th0):
t0 = 2*np.pi*(l / g)**0.5 / 4
t = fsolve(pendulum_th, t0, args = (l, th0))
return t * 4
fsolve()求解时需要一个初始值尽量接近真实的解。用小角度单摆的周期的$frac{1}{4}$作为这个初始值是一个很不错的选择。下面利用pendulum_period()计算出初始摆动角度从0到90度的摆动周期:
ths = np.arange(0, np.pi/2.0, 0.01)
periods = [pendulum_period(1, th) for th in ths]
代码中首先对角度进行初始化,得到一个等分序列ths,接着用该序列以及pendulum()函数进行求解。
为了验证fsolve()求解摆动周期的正确性,下面的公式是从维基百科中找到的摆动周期的精确解:
其中的函数K为第一类完全椭圆积分函数,定义如下:
\[\begin{equation} K(k)=\int_0^{\pi/2}\frac{d\theta}{\sqrt{1-k^2sin^2\theta}} \end{equation}\]可以用scipy.special.ellipk()计算此函数的值:
from scipy.special import ellipk
periods2 = 4 * (1.0 / g)**0.5 * ellipk(np.sin(ths / 2) **2 )
periods2则是对公式(13)的定义。
接下俩的代码是对两种方法的结果比较:
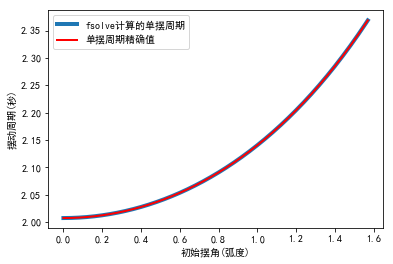
#%fig=单摆的摆动周期和初始角度的关系
ths = np.arange(0, np.pi/2.0, 0.01)
periods = [pendulum_period(1, th) for th in ths]
periods2 = 4 * (1.0/g)**0.5 *ellipk(np.sin(ths/2)**2) # 计算单摆周期的精确值
pl.plot(ths, periods, label = u"fsolve计算的单摆周期", linewidth=4.0)
pl.plot(ths, periods2, "r", label = u"单摆周期精确值", linewidth=2.0)
pl.legend(loc='upper left')
pl.xlabel(u"初始摆角(弧度)")
pl.ylabel(u"摆动周期(秒)");
结果如下图所示: