论文原文:A Simple but Tough-to-beat Baseline for Sentence Embeddings,论文实现代码(由论文作者提供):code。
花了两天时间来看这篇论文,现在来记录下,还没有开始看代码,等后面有空看完代码再写个续集。o^v^o~
Abstract
这篇论文提出了SIF sentence embedding方法,该方法可以利用像Wikipedia这样无标签的语料库,通过词向量的加权平均来表示句子,然后利用PCA或者SVD对其进行一些修改。在本文相似性任务中,这种加权方式能够提升10%~30%的性能。这个简单的方法能够作为将来的训练基准,特别是在有标签的训练数据稀少或不存在的情况下。论文中还给出了用潜在变量生成模型对句子进行无监督训练的理论解释。
Introduction
(Bengio et al., 2003; Collobert & Weston, 2008; Mikolov et al., 2013a; Pennington et al., 2014): Word bedding计算作为NLP和IR中的基础构造块,捕捉词与词之间的相似度。
(Iyyer et al., 2015; Le & Mikolov, 2014; Kiros et al., 2015; Socher et al., 2011; Blunsom et al., 2014; Tai et al., 2015; Wang et al., 2016): 最近的工作有尝试计算embeddings,可以捕捉paraphrastic(短语、句子、词组)中的情感,这些方法从简单的词向量叠加到复杂结构,例如卷积神经网络(CNN)和循环神经网络(RNN)。
近期,(Wieting et al., 2016)研究一般用途,在数据集(PPDB)中他开始用标准word embedding以及在有监督的情况下进行修正paraphrastic embedding,并且通过训练简单的word averaging model来构建sentence embeddings。这个简单方法在文本相似性上比各种各样的方法有更好的表现,并且可以作为文本分类任务的良好初始化。但是有监督的数据集短语是至关重要的,因为他们反应了初始word embedding的简单平均值并没有很好的效果。
接下来引出该论文的研究内容:仅仅计算句子中词向量的权重值,然后一处平均向量在其第一奇异向量上的投影(common component removal,公共分量移除)。词的权重计算计算公式:
\[\begin{equation} \omega=\frac{a}{a+p(\omega)} \end{equation}\]其中,$a$是一个参数,$p(\omega)$是词频(估计值);我们称这个叫做smooth inverse frequency(SIF)。这个方法在各种各样的文本相似性任务上比无权重均值效果更好,并且在(Wieting et al. 2016)的试验中,这个方法甚至能够打败一些复杂的有监督方法,例如RNN和LSTM模型。这个方法更适合域适应设置,在各种各样的语料库中训练过的词向量在不同的试验台下对计算sentence embedding很有用。该算法对加权方案(weighting scheme)也也具有较强的鲁棒性(robust): 使用不同语料库中的词频率估计不会影响性能;参数$a$的范围较宽,可以比未加权平均值有显著的提高。
Related Works
Word embedding
word embedding将词表示为低维空间中的连续向量,捕捉词汇和语义特性,它们可以从文本的神经网络模型的内部表示得到(Bengio et al., 2003; Collobert & Weston, 2008; Mikolov et al., 2013a)或通过共现统计学的低秩近似(Deerwester et al., 1990; Pennington et al., 2014)。这两种方法是密切相关的(Levy & Goldberg, 2014; Hashimoto et al., 2016; Arora et al., 2016)。
Phrase/Sentence/Paragraph embeddings
以往的研究都是利用向量和矩阵的操作来组合word embedding从而计算phrase or sentence embedding。(Mitchell & Lapata, 2008; 2010; Blacoe & Lapata, 2012)。其中coordinate-wise multiplication表现得很好。非加权平均对短语的表示方面做得很好(Mikolov et al., 2013a)。
另一种方法是在解析树上定义的递归神经网络(RNNs),监督学习(Socher et al., 2011) 或者非监督 (Socher et al., 2014)。简单的RNNs可以看作是解析树被简单的线性链替换的特殊情况。
(Mikolov et al., 2013b):Skip-gram模型被扩展为合并序列的潜在向量,或将序列视为一个基础单元。
(Le & Mikolov, 2014) :每个段落假设有一个潜在段落向量,影响段落中每个词的分布。
(Kiros et al., 2015):Skip-thought重构某个句子周围的句子,将隐藏参数视为向量表示。
(Tai et al., 2015):RNNs使用LSTM捕捉长距离依赖,用于建模句子。
(Blunsom et al., 2014):CNN,使用动态pooling来处理变长句子,在语义预测和分类任务中表现良好。
A Simple Method for Sentence Embedding
我们简单的回顾了latent variable generative model(Aroal al.,2016)。模型把生成过程看作是一个动态的过程,在这个过程中,第t个词是在步骤t中产生的。这个过程甚至是通过discourse vector $c_t\in{\mathfrak{R}^d}$。每个在单词表中的单词$\omega$也有一个向量$\mathfrak{R}^d$;这些都是模型的潜在变量。这个discourse vector载体代表着“谈论的含义是什么”。discourse vector $c_t$和(时间不变量,time-invariant)词向量$\omega$之间的内积表示语篇和词之间的相关性。用Mnih和Hinton的对数线性词产生模型(log-linear word production model)给出了在$t$时刻观察到词$\omega$的概率:
\[\begin{equation} Pr[\omega\ emitted\ at\ time\ t\ \mid {c_t}]\propto{exp(\langle{c_t, v_\omega}\rangle)} \end{equation}\]discourse vector $c_t$做缓慢的随机游走(random walk),也就是说,$c_{t+1}$是由$c_t$加上小的随机位移向量得到的,从而在相思的雨偏下生成邻近的词。在(Arora et al.,2016)中表明,在一些合理的假设下,该模型产生的单词词共现概率符合Word2VecandGlove等经验主义著作。由于简单的计算表明随机游走模型对词的共现概率的影响可以忽略不计,因此可以放宽随机游走模型,允许$c_t$中偶尔出现较大的跳跃,用该模型计算的词向量与glove和word2vec(CBOW)的相似。
Our improved Random Walk model
将sentence embedding定义成如下很有诱惑力:给定一个句子$s$,对支配这个句子的discourse vector做一个映射估计(MAP estimate)。假设discourse vector:在句子中的单词被发出时的变化不大,因此我们可以用一个discourse vector $c_s$来代替句子中所有的$c_t$。
该篇论文中,为了更真实地建模,我们将模型(1)更改如下。这个模型有两种类型的“平滑词”,这是为了解释这样一个事实:有些词出现在语境之外,而有些频繁出现的词(可能是“the”、“and”等)则经常出现在不考虑话语的情况下。我们首先在对数线性模型中引入了一个加法项$\alpha{p(\omega)}$,其中$p(\omega)$是单词地一元模型(unigram)概率(在整个语料库中)并且$\alpha$是一个标量。这使得词的向量与$c_s$的内积很小,其次,引入一个普通的discourse vector $c_0\in{\mathfrak{R}^d}$,它是对经常与语法相关的最频繁语篇的一个修正项。(其他可能的修正留给以后研究)。它提升了$c_0$与高成分词的贡献概率。
具体来说,给定discourse vector $c_s$,一个单词$\omega$的概率在句子$s$中被释放出来:
\[\begin{equation} Pr[\omega\ emitted\ in\ sentence\ s\mid{c_s}] = \alpha{p(\omega)}+(1-\alpha)\frac{exp(\langle{\widetilde{c}_s,v_\omega}\rangle)}{Z_{\widetilde{c}_s}}, \\ where\ \widetilde{c}_s=\beta{c_0}+(1-\beta)c_s, c_0\perp{c_s} \end{equation}\]其中,$\alpha$和$\beta$都是标量超参数,并且$ Z_ {\widetilde{c}_ s}=\sum_ {\omega\in{\nu}}exp(\langle{\widetilde{c}_ s,v_ \omega}\rangle)$ 是标准化常数(配分函数),我们看到模型允许一个与discourse vector $c_s$不相关的的单词$\omega$被发出有两个原因: 1)来自于术语$\alpha{p(\omega)}$的偶然;2)如果$\omega$与公共discourse vector $c_0$相关。
综上所述,算法简单来说如下所示:

注:该图片来源于博客:Hsiao,该图片最初来源于陈丹琦女士在斯坦福分享的PPT。
-
W 步:对于句子中的每个词向量乘以一个独特的权值,即$\frac{a}{a+p(\omega)}$,其中$a$为一个常数 (论文中建议$a$的范围:$[1e−4,1e−3]$),$p(\omega)$为该词的频率。
-
R 步:计算语料库所有句向量构成的矩阵的第一个主成分 $u$,让每个句向量减去它在$u$上的投影 (类似 PCA)。其中,一个向量$v$在另一个向量$u$上的投影定义为:$Proj_{u}v=\frac{uu^Tv}{\Vert{u}\Vert^2}$。
概率论解释:
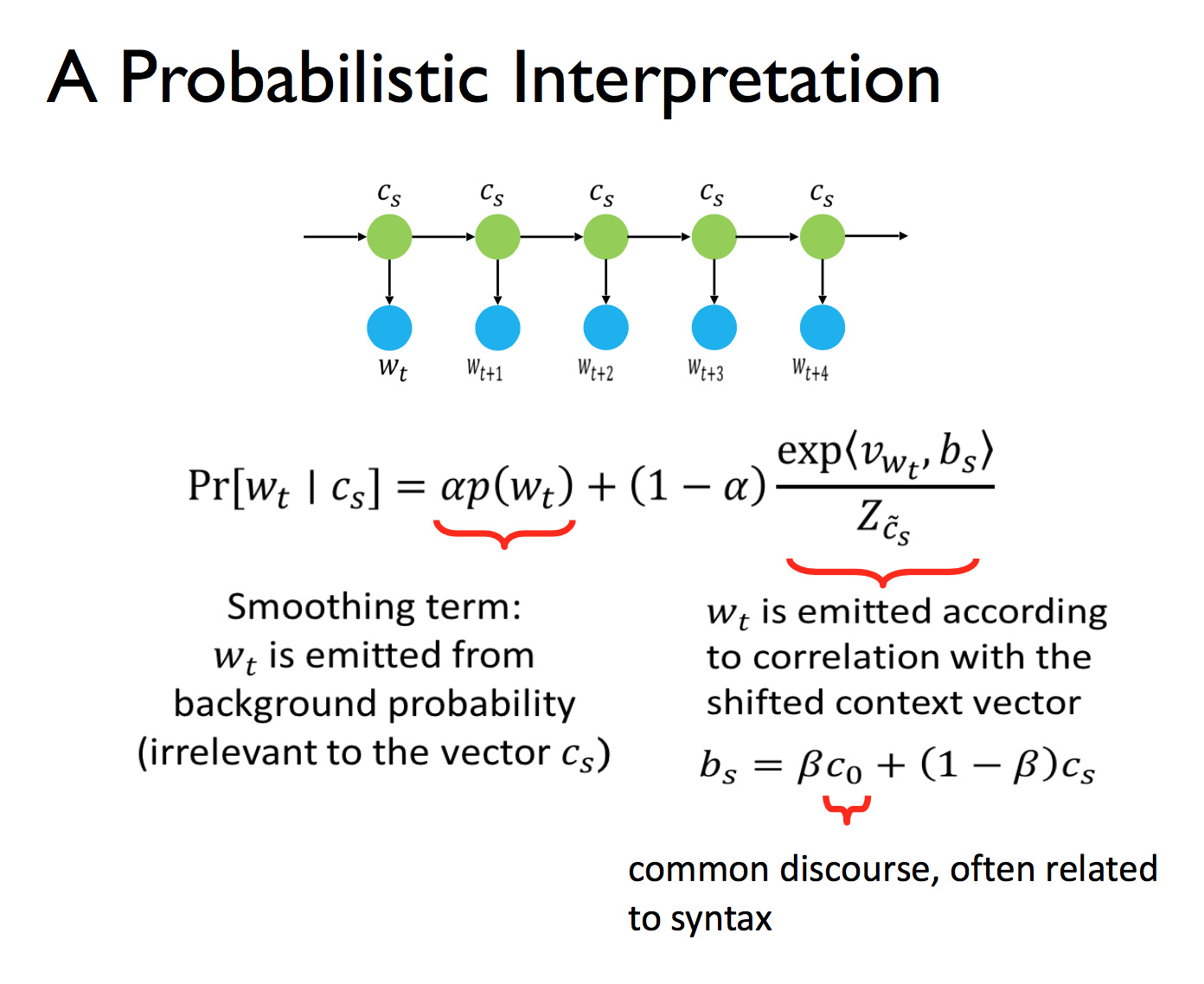
注:该图片来源于博客:Hsiao,该图片最初来源于陈丹琦女士在斯坦福分享的PPT。
其原理是,给定上下文向量,一个词的出现概率由两项决定:1)作为平滑项的词频,2)上下文。公式第二项的意思是,有一个动态平滑的上下文随机地发出单词。
算法流程如下:

注:该图片来源于原论文。
Computing the sentence embedding
由模型生成word embedding实际上是同步的。the sentence embedding被定义为生成它的向量$c$的最大似然估计。(在本例中,MLE与MAP是相同的,因为前者是一致的)。借用(Arora et al.,2016)的关键的建模假设,即单词$v_\omega$大致是均匀分布的,这意味着分区函数$Z_c$在所有方向上都大致相同。所以假定$Z_{\widetilde{c}_s}$大致相同,说$Z$能代替所有的$\widetilde{c}_s$。根据模型2,这些内容的可能性为:
\[\begin{equation} p[s\mid{c_s}]=\prod_{\omega\in{s}}p(\omega\mid{c_s})=\prod_{\omega\in{s}}[\alpha{p(\omega)}+(1-\alpha)\frac{ exp(\langle{v_\omega, \widetilde{c}_s}\rangle) }{Z}] \end{equation}\]令:
\[\begin{equation} f_\omega(\widetilde{c}_s)=log[\alpha{p(\omega)}+(1-\alpha)\frac{ exp(\langle {v_\omega, \widetilde{c}_s} \rangle) }{Z}] \end{equation}\]表示句子$s$的对数似然。接着通过简单的演算可得到:
\[\begin{equation} \bigtriangledown{f_\omega(\widetilde{c}_s)} =\frac{1}{\alpha{p(\omega)}+(1-\alpha)\frac{ exp(\langle {v_\omega, \widetilde{c}_s} \rangle) }{Z}}\frac{1-\alpha}{Z}exp(\langle {v_\omega, \widetilde{c}_s} \rangle)v_\omega \end{equation}\]接着通过泰勒展开,可得:
\[\begin{equation} f_\omega(\widetilde{c}_s)\approx f_\omega(0)+\bigtriangledown{f_\omega(0)^T\widetilde{c}_s}\\ =constant+\frac{(1-\alpha)/(\alpha{Z})}{p(\omega)+(1-\alpha)/(\alpha{Z})} \langle v_\omega, \widetilde{c}_s \rangle \end{equation}\]因此,单位球面(unit sphere, 原文是这样,翻译感觉怪怪的)$\widetilde{c}_s$的极大似然估计(忽略正规化)是大约为:
\[\begin{equation} arg\ max\sum_ {\omega\in{s}}f_ \omega(\widetilde{c}_s)\propto{ \sum_{\omega\in{s}}\frac{a}{p(\omega)+a}v_\omega }, where\ a=\frac{1-\alpha}{\alpha{Z}} \end{equation}\]因此,MLE是句子中词向量的权重近似均值。注意对于更频繁的单词$\omega$,权重$\frac{a}{p(\omega)+a}$会更小,因此这自然导致频繁单词投影到其第一主成分的权重降低。
为了估计$c_s$,我们通过计算一组句子中$\widetilde{c}_s$的第一主成分来估计$c_0$的方向。换言之,最后的sentence embedding是通过将$\widetilde{c}_s$的投影减去其第一主成分得到的。算法一总结了这一点。
因此可以得到:
-
最优解为句子中所有单词向量的加权平均;
-
对于词频更高的单词$\omega$, 权值更小, 因此这种方法也等同于下采样频繁单词。
Experiments
结果
-
对比算法结果

注:该图片来源于原论文。
-
加权参数对性能的影响
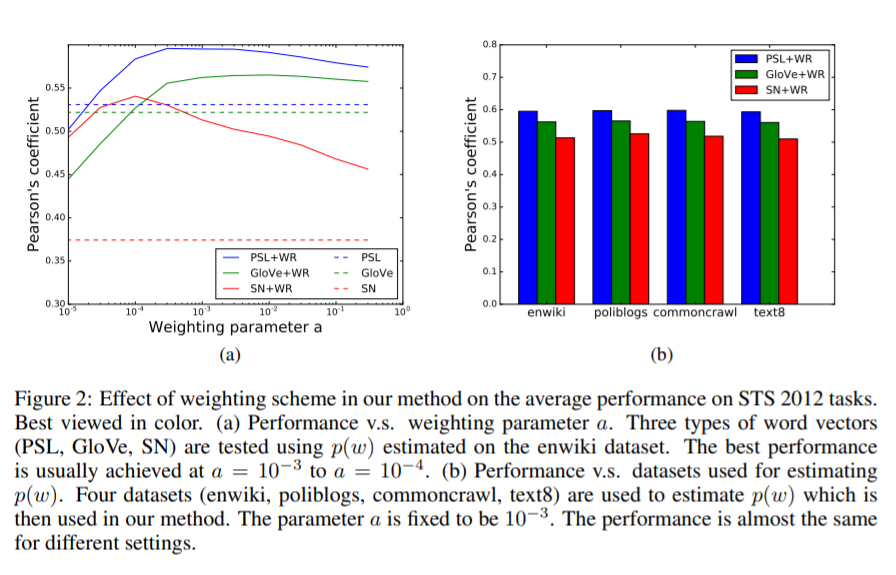
注:该图片来源于原论文。
(a)表明加权参数a的调整比非加权平均有显著的提升。
(b)表明性能在四个数据集上表现差不多。
说明本文算法能够应用于不同类型的,在不同语料库中训练的词向量。跨领域性强。
监督任务
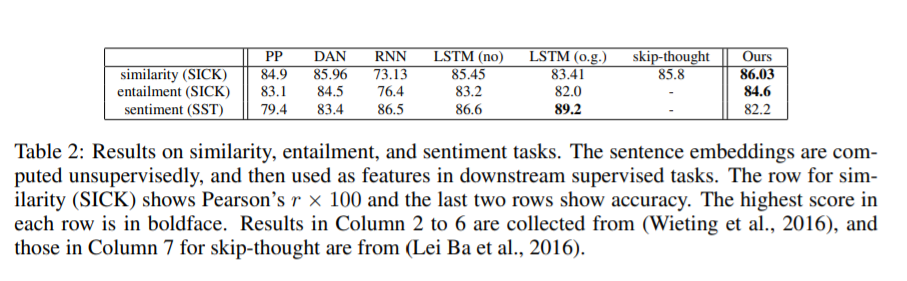
注:该图片来源于原论文。
本文算法在两项任务中表现最好。但是在第三个任务上表现没有RNN和LSTM好,原因:
词向量,或者说意义分布假说,由于反义词问题,在捕捉语义方面有局限性。解决方法:(Maas et al., 2011)为语义分析学习更好的词嵌入 “not”等单词在语义分析中可能是很重要的。解决方法:为这个特殊的任务设计权重方案
句子中单词顺序带来的影响
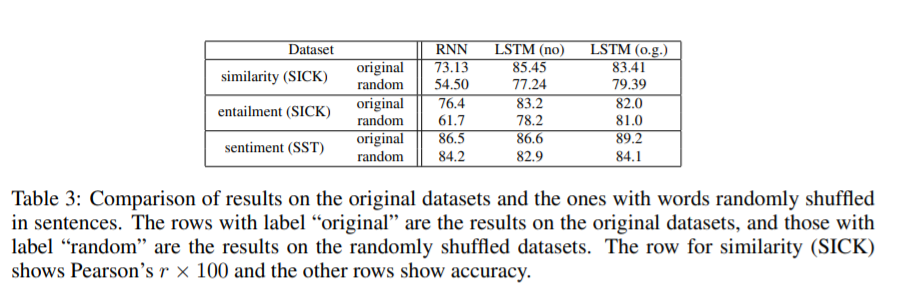
注:该图片来源于原论文。
参考文献:
http://hellojet.cn/2018/12/17/%E8%AE%BA%E6%96%87%E9%98%85%E8%AF%BB%EF%BC%9AA%20Simple%20but%20Tough-to-beat%20Baseline%20for%20Sentence%20Embeddings/
https://www.cnblogs.com/databingo/p/9788244.html
https://hsiaoyetgun.github.io/2018/05/06/CS224n%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0%20Research%20Highlight1%20A%20simple%20but%20tough-to-beat%20baseline%20for%20sentence%20embedding/
http://www.hankcs.com/nlp/cs224n-sentence-embeddings.html
这是中秋之前打算写完的博客,结果因为中间有比赛耽搁了,比完赛还没休息就赶紧来补博客了。