- Plotting univariate distributions
- Plotting bivariate distributions
- Visualizing pairwise relationships in a dataset
有关分类变量的绘制
处理数据时,我们一定会希望在做分析或者处理前能够了解数据的分布情况。
导入所需的包:
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats
sns.set(color_codes=True)
Plotting univariate distributions
用seaborn最快能查看数据分布的函数是distplot()。默认情况下,它绘画直方图并且加上KDE。
x = np.random.normal(size=100)
sns.distplot(x)
结果如下图所示:

Histograms
直方图就是统计落在不同范围内的观测值数量,同时可以增加rug plot。
sns.distplot(x, kde=False, rug=True)
结果如下图所示:
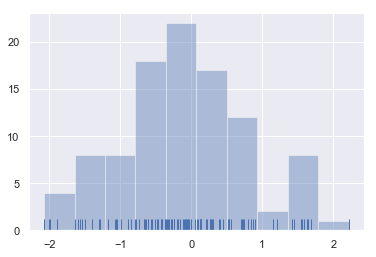
绘制直方图时,主要需要选择分组的数量和位置,distplot()默认会利用简单规则猜测更为适合的数字,可以尝试更多或者更少的条来显示数据中的其他维度。
sns.distplot(x, bins=20, kde=False, rug=True)
结果如下图所示:
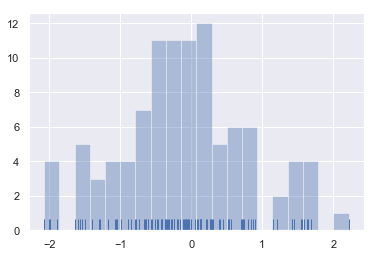
Kernel density estimation
KDE可以很好的表现数据的分布情况。
sns.distplot(x, hist=False, rug=True)
结果如下图所示:
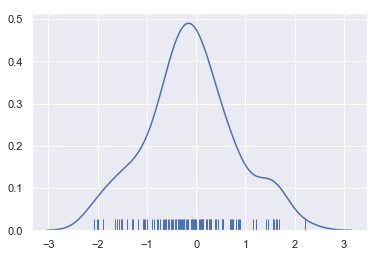
绘制一个KDE比直方图计算更为复杂,因此我们首先用值为中心的高斯曲线替换每个观测值:
x = np.random.normal(0, 1, size=30)
bandwidth = 1.06 * x.std() * x.size ** (-1 / 5.)
support = np.linspace(-4, 4, 200)
kernels = []
for x_i in x:
kernel = stats.norm(x_i, bandwidth).pdf(support)
kernels.append(kernel)
plt.plot(support, kernel, color="r")
sns.rugplot(x, color=".2", linewidth=3)
结果如下图所示:

接下来,对曲线求和,以计算支撑网格中每个点的密度值,然后将得到的曲线规格化,是其下的面积等于1:
from scipy.integrate import trapz
density = np.sum(kernels, axis=0)
density /= trapz(density, support)
plt.plot(support, density)
结果如下图所示:
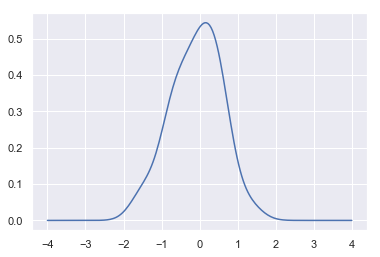
同时,可以用函数kdeplot()来得到相同的曲线:
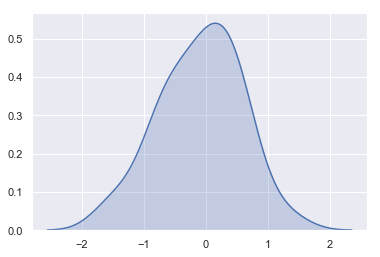
sns.kdeplot(x, shade=True)
结果如下图所示:
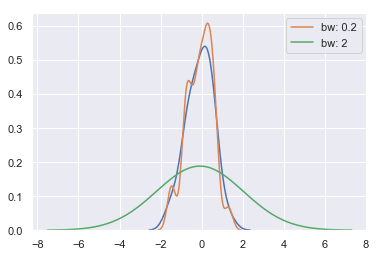
在KDE函数中有一个参数“bandwidth(bw)”来设置曲线对数据的贴合程度:值越大,曲线越平滑,贴合程度越小;值越大,曲线越曲折,贴合程度越大。(该参数在violinplot()也用到过,violin函数也包含KDE的效果)
sns.kdeplot(x)
sns.kdeplot(x, bw=.2, label="bw: 0.2")
sns.kdeplot(x, bw=2, label="bw: 2")
plt.legend()
结果如下图所示:
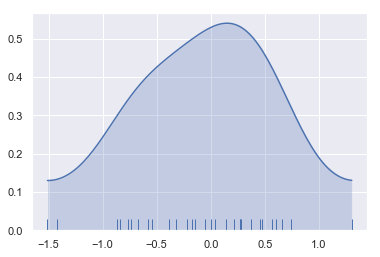
如上所示,高斯KDE过程的性值意味着估计超过了数据集中的最大值和最小值。可以使用CUT参数绘制曲线时,控制曲线超过极值的程度,这个参数只是影响曲线的绘制方式,而不影响曲线的拟合方式。
sns.kdeplot(x, shade=True, cut=0)
sns.rugplot(x)
结果如下图所示:
Fitting parametric distributions
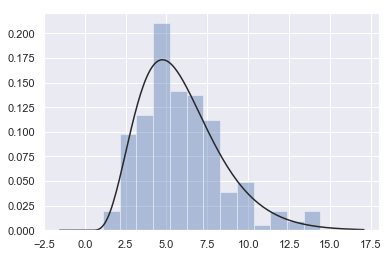
你可以用函数distplot()来拟合数据集分布的参数,并直观的评估与观察到的数据的对应程度:
x = np.random.gamma(6, size=200)
sns.distplot(x, kde=False, fit=stats.gamma)
结果如下图所示:
Plotting bivariate distributions
上面都是对一个变量的分布情况进行描述,同样的,也可以绘制两个变量的二元分布。在seaborn中最简单的方法是使用函数jointplot(),他创建一个多面板图形,显示两个变量之间二元关系以及每个变量在单独轴上的一元分布(边缘分布)。
导入数据:
mean, cov = [0, 1], [(1, .5), (.5, 1)]
data = np.random.multivariate_normal(mean, cov, 200)
df = pd.DataFrame(data, columns=["x", "y"])
Scatterplots
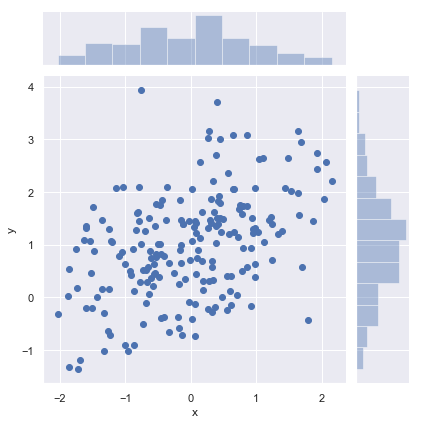
最常见的可视化二元分布的是散点图,其中每个观察点都显示在x和y值出。这是对两个维度的rug plot展示,可以使用matplotlib.scatter函数绘制散点图,它也是函数jointplot()的默认类型图:
sns.jointplot(x="x", y="y", data=df)
结果如下图所示:
Hexbin plots
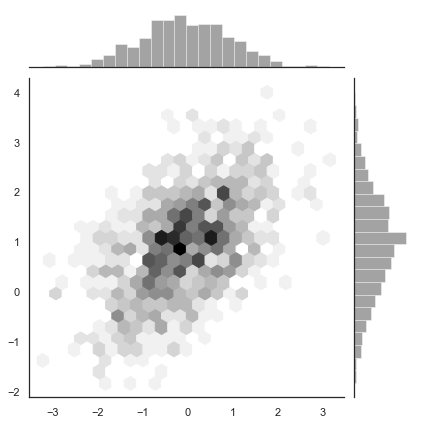
可以将点换成一个六边形,此图适用于相对较大的数据集。它可以通过matplotlib.hexbin函数和jointplot()中的样式获得,白色背景更好:
x, y = np.random.multivariate_normal(mean, cov, 1000).T
with sns.axes_style("white"):
sns.jointplot(x=x, y=y, kind="hex", color="k")
结果如下图所示:
Kernel density estimation
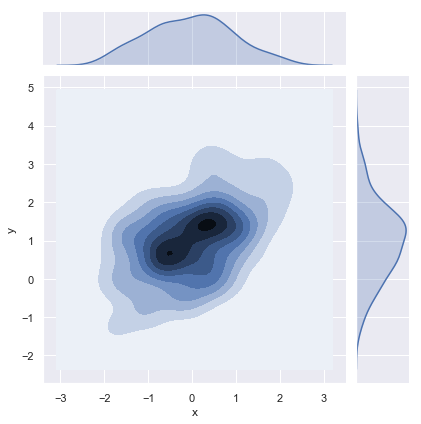
它也可以使用上面描述的KDE过程来可视化二元分布。在Seaborn中,此类绘图显示为等高线图,并在jointplot()中作为样式提供:
sns.jointplot(x="x", y="y", data=df, kind="kde")
结果如下图所示:
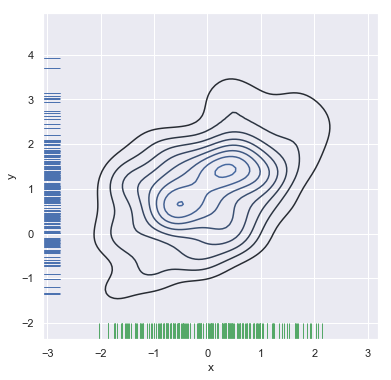
还可以使用kdeplot()函数绘制二维内KDE图。这能够将这种绘图绘制到一个特定的maplotlib轴上,用函数jointplot()来管理自己figure:
f, ax = plt.subplots(figsize=(6, 6))
sns.kdeplot(df.x, df.y, ax=ax)
sns.rugplot(df.x, color="g", ax=ax)
sns.rugplot(df.y, vertical=True, ax=ax)
结果如下图所示:
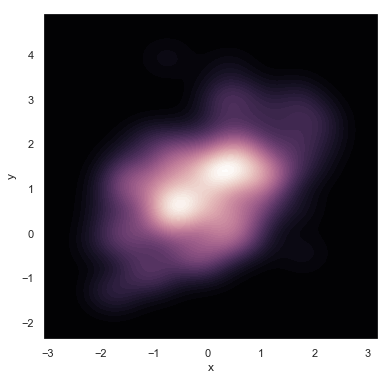
如果想更连续的展示数据的密度,可以简单的增加等高线层数:
f, ax = plt.subplots(figsize=(6, 6))
cmap = sns.cubehelix_palette(as_cmap=True, dark=0, light=1, reverse=True)
sns.kdeplot(df.x, df.y, cmap=cmap, n_levels=60, shade=True)
结果如下图所示:
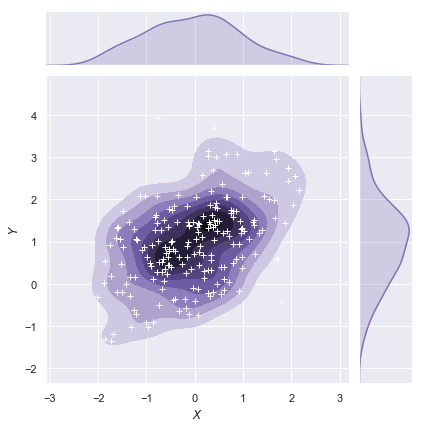
函数jointplot()用JointGrid类来管理figure:
g = sns.jointplot(x="x", y="y", data=df, kind="kde", color="m")
g.plot_joint(plt.scatter, c="w", s=30, linewidth=1, marker="+")
g.ax_joint.collections[0].set_alpha(0)
g.set_axis_labels("$X$", "$Y$")
结果如下图所示:
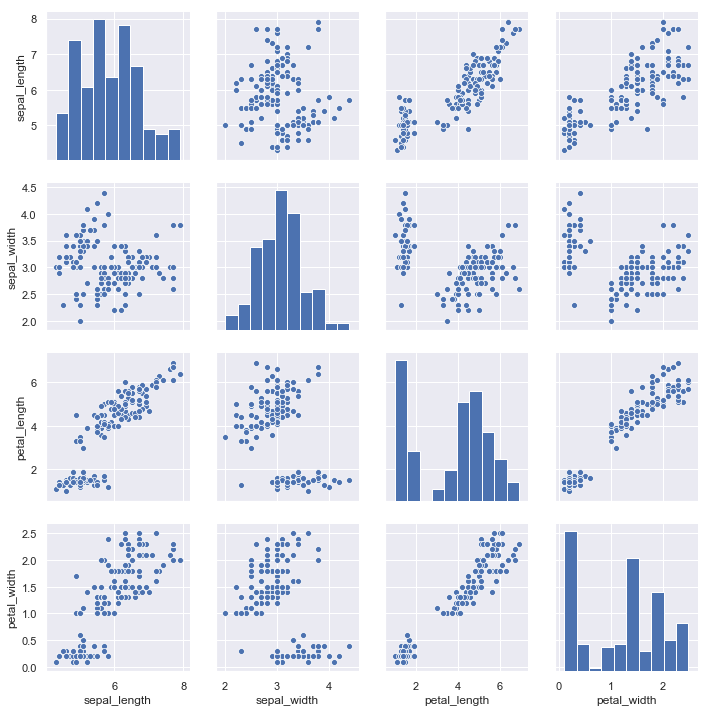
Visualizing pairwise relationships in a dataset
生成多对的二元分布,可以使用函数pairplot():
iris = sns.load_dataset("iris")
sns.pairplot(iris)
结果如下图所示:
函数pairplot()建立在类PairGrid上,我们可以更加灵活的使用它:
g = sns.PairGrid(iris)
g.map_diag(sns.kdeplot)
g.map_offdiag(sns.kdeplot, n_levels=6)
结果如下图所示:

参考文献:
http://seaborn.pydata.org/tutorial/distributions.html