- Functions to draw linear regression models
- Fitting different kinds of models
- Conditioning on other variables
- Controlling the size and shape of the plot
- Plotting a regression in other contexts
大部分数据集包含多个变量,分析的目标通常是将这些变量相互关联,之前通过显示两个变量之间的joint distribution实现了这一目的。但是用统计模型来估计两组噪声观测值之间的简单关系是非常有用的。
Seaborn主要是一个在探索数据、分析数据中帮我们在视觉上进行强调而不是对数据进行分析。因此要获得与回归模型拟合相关的定量度量应该使用statsmodels包。
首先导入需要用到的包:
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
#set the options(global) of Seaborn.
sns.set(color_codes=True)
#load data.
tips = sns.load_dataset("tips")
Functions to draw linear regression models
用来可视化通过回归确定线性关系的两个主要函数:regplot()、lmplot()。
在简单的调用中,两个函数都会绘制一个x和y两个变量的散点图,然后拟合回归模型y~x,并绘制出回归线和该回归的95%置信区间:
sns.regplot(x="total_bill", y="tip", data=tips)
结果如下图所示:
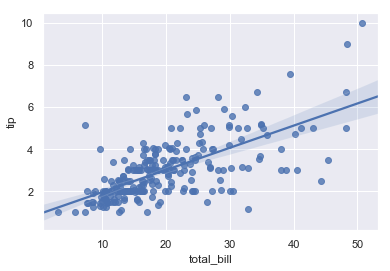
sns.lmplot(x="total_bill", y="tip", data=tips)
结果如下图所示:
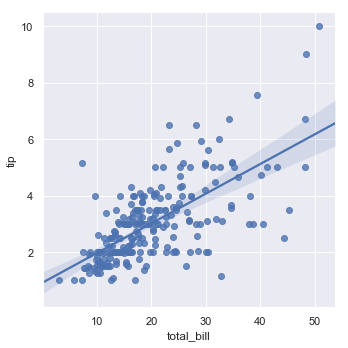
上面绘制出的两个图是相同的,仅仅是图形的形状有所差异。另一个主要的差异是:regplot()接受各种格式的x、y变量(numpy, Series(in Pandas), DataFrame(in Pandas)中变量的引用)。相反,lmplot()将数据作为必需参数,x、y变量必须指定为字符串。这个数据格式称为“long-form”或者“tidy”。除了输入的灵活性外,regplot()拥有lmplot()特性的子集。
当其中一个变量取离散值时,可以拟合线性回归,但是,此类数据集生成的简单散点图通常不是最优的:
sns.lmplot(x="size", y="tip", data=tips)
结果如下图所示:
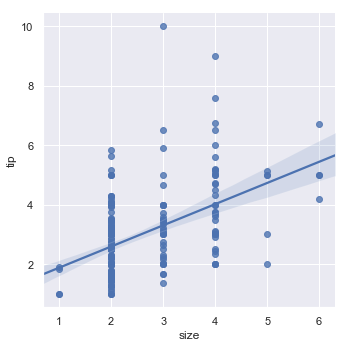
一个选择是增加一个随机噪声”jitter”来分离值,从而使得值的分布更加清晰。jitter仅应用于散点图数据,不影响回归线拟合本身。
sns.lmplot(x="size", y="tip", data=tips, x_jitter=.05)
结果如下图所示:
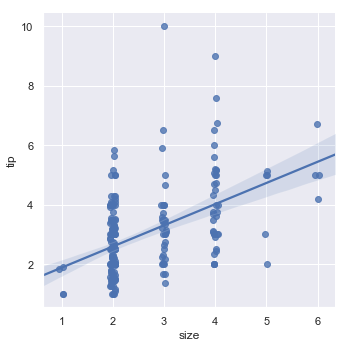
第二个选择是折叠在每个离散区间中的观测值,以绘制中心趋势的估计值和置信区间(通过x_estimator参数进行设置)。
sns.lmplot(x="size", y="tip", data=tips, x_estimator=np.mean)

Fitting different kinds of models
上述简单线性回归模型的拟合非常简单,但不适合于某些类型的数据集。The Anscombe’s quarter数据集展示了几个例子,其中简单的线性回归提供了对关系的相同估计,其中简单的视觉检查清楚地显示了差异例如,在第一种情况下,线性回归是一个很好的模型:
#load dataset
#anscombe = sns.load_dataset("anscombe")
anscombe = pd.read_csv(r'D:\Desktop\专业课\数据可视化\seaborn_data\anscombe.csv')
注:我加载失败了就直接用pandas包中的read_csv()函数加载了本地数据集。
sns.lmplot(x="x", y="y", data=anscombe.query("dataset == 'I'"),
ci=None, scatter_kws={"s": 80})
结果如下图所示:

在第二个数据集中同样使用了线型拟合,但是从图中我们看到这并不是一个好模型:
sns.lmplot(x="x", y="y", data=anscombe.query("dataset == 'II'"),
ci=None, scatter_kws={"s": 80})
结果如下图所示:
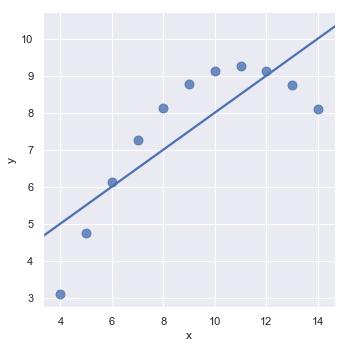
在这种高阶关系,lmplot()和regplot()可以拟合一个多项式回归模型来探索数据集中的简单非线性趋势:
sns.lmplot(x="x", y="y", data=anscombe.query("dataset == 'II'"),
order=2, ci=None, scatter_kws={"s": 80})
结果如下图所示:

另一个问题是“异常值”由于某些原因偏离研究的主要关系:
sns.lmplot(x="x", y="y", data=anscombe.query("dataset == 'III'"),
ci=None, scatter_kws={"s": 80})
结果如下图所示:
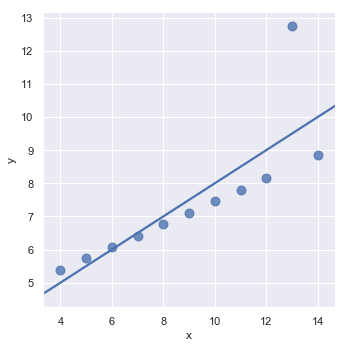
存在异常值的情况下,拟合一个稳健回归很有用,它使用不同的损失函数来降低相对较大的残差(使用参数robust):
sns.lmplot(x="x", y="y", data=anscombe.query("dataset == 'III'"),
robust=True, ci=None, scatter_kws={"s": 80})
结果如下图所示:
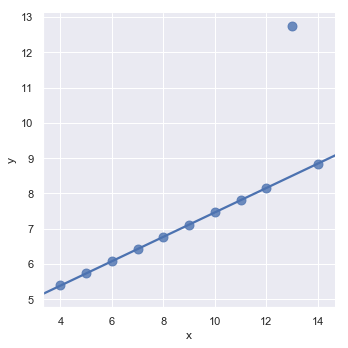
当变量y是二元变量时,简单的回归将会给出不可信的预测:
tips["big_tip"] = (tips.tip / tips.total_bill) > .15
sns.lmplot(x="total_bill", y="big_tip", data=tips,
y_jitter=.03)
结果如下图所示:
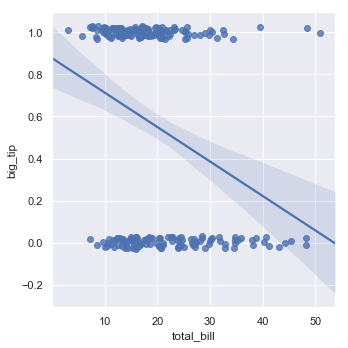
针对于这种情况解决方案是拟合一个Logistic regression,这昂回归线显示给定值x的y=1的估计概率(使用参数logistic):
sns.lmplot(x="total_bill", y="big_tip", data=tips,
logistic=True, y_jitter=.03)
结果如下图所示:
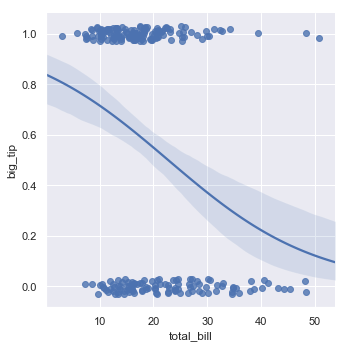
相对于简单回归,Logistic Regression计算的复杂度将会高很多(这也适用于稳健回归),并且回归线周围的置信区间是使用bootstrap过程计算的,可以选择关闭该选项以加快迭代速度(使用ci=None):
sns.lmplot(x="total_bill", y="tip", data=tips,
lowess=True)
结果如下图所示:
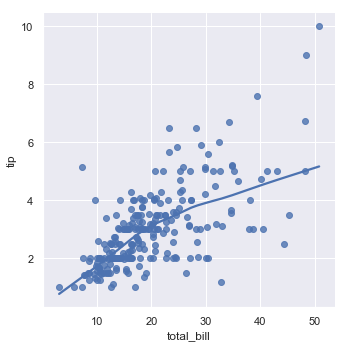
函数residplot()的作用是检查简单回归模型是否适合数据集。它拟合并删除一个简单的线性回归,然后绘制每个观测值的残值理想情况下,这些值应该随机分布在”y=0”周围:
sns.residplot(x="x", y="y", data=anscombe.query("dataset == 'I'"),
scatter_kws={"s": 80})
结果如下图所示:
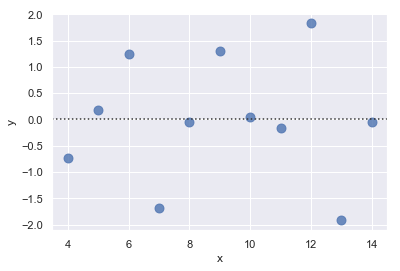
如果残差中存在结构(这里翻译的有点奇怪,类似于趋势的意思),则表明简单线性回归不适合:
sns.residplot(x="x", y="y", data=anscombe.query("dataset == 'II'"),
scatter_kws={"s": 80})
结果如下图所示:
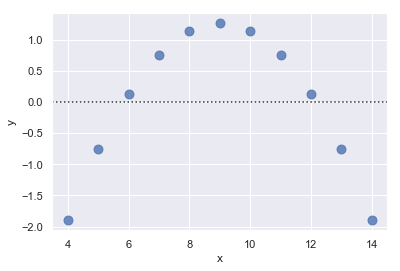
Conditioning on other variables
上面的图都是展示的两个变量之间的关系,若是增加一个变量又会如何?这也就是regplot()和lmplot()两个函数有区别的地方。函数regplot()总是展示单一关系,lmplot() 包含了regplot()和FacetGrid结合起来提供了一个简单的界面来显示“faceted plot”,允许探索三个分类变量关系。
分开关系的最好的方法就是在相同的axes中以不同的颜色来区分不同关系。
sns.lmplot(x="total_bill", y="tip", hue="smoker", data=tips)
结果如下图所示:
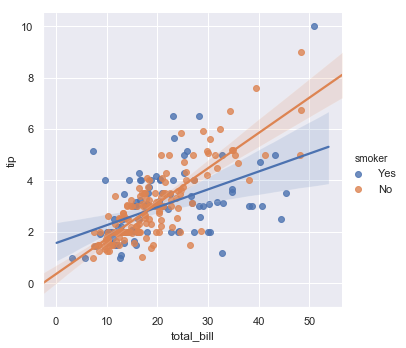
除了颜色之外,还可以使用不同的标记画散点,这样可以更好的在黑白打印的时候展现出图中变量的差异,并且可以完全自己设置颜色:
sns.lmplot(x="total_bill", y="tip", hue="smoker", data=tips,
markers=["o", "x"], palette="Set1")
结果如下图所示:
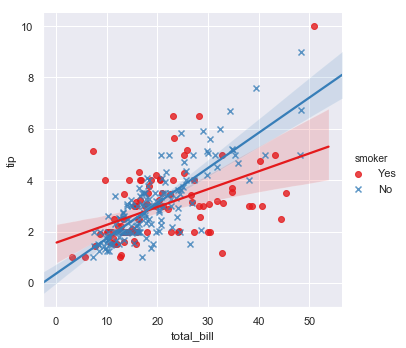
想要增加其他的变量时你可以画多个“facets”,其中每个level的变量都显示在网格的行或列中。
sns.lmplot(x="total_bill", y="tip", hue="smoker", col="time", data=tips)
结果如下图所示:
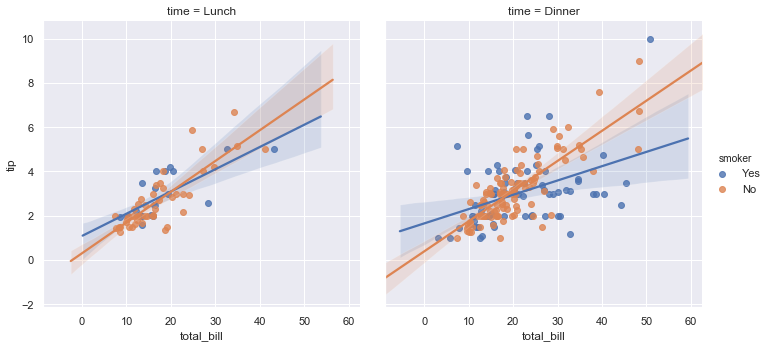
sns.lmplot(x="total_bill", y="tip", hue="smoker",
col="time", row="sex", data=tips)
结果如下图所示:
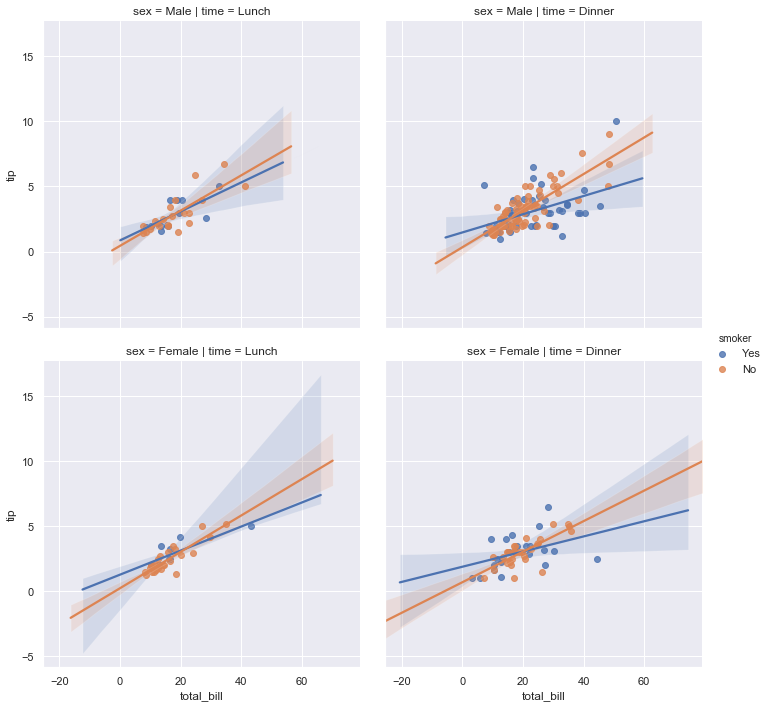
Controlling the size and shape of the plot
函数regplot()和lmplot()画出的图看起来是一样的,但是它们默认图的大小却是有差别。这是因为函数regplot()是一个绘制到特定轴的”axes-level”函数,这意味着可以自己制作 multi-panel图,并且可以精确控制回归图的位置。如果不显示提供axes对象,则它只是用“currently active” axes,这就是默认绘图的大小与大多数其他matplotlib函数具有相同大小和形状的原因。如果要控制它的大小,需要创建一个figure对象。
f, ax = plt.subplots(figsize=(5, 6))
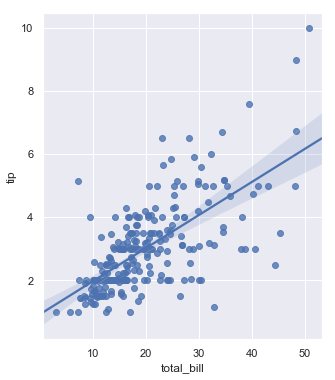
sns.regplot(x="total_bill", y="tip", data=tips, ax=ax)
结果如下图所示:
相对的,函数lmplot()绘制图的大小和尺寸是通过FacetGrid接口中的”size”和”aspect”参数来控制的,这些参数应用于图中的每个facet,而不是整个图形本身。
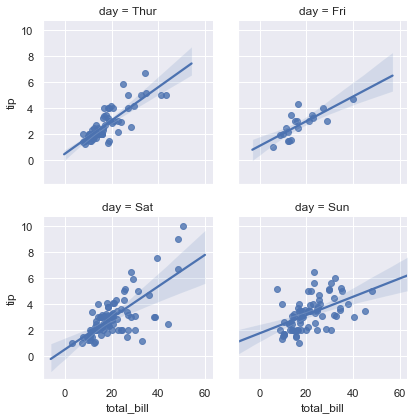
sns.lmplot(x="total_bill", y="tip", col="day", data=tips,
col_wrap=2, height=3)
结果如下图所示:
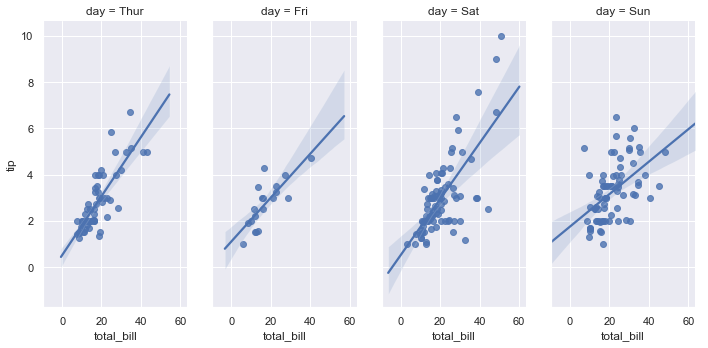
sns.lmplot(x="total_bill", y="tip", col="day", data=tips,
aspect=.5)
结果如下图所示:
Plotting a regression in other contexts
其他一些seaborn函数在更大、更复杂的环境下使用函数regplot(),比如函数jointplot()。除了之前的风格,jointplot()函数还可以用函数regplot()通过传递参数”kind=’reg’“在joint axes展示线性回归拟合。
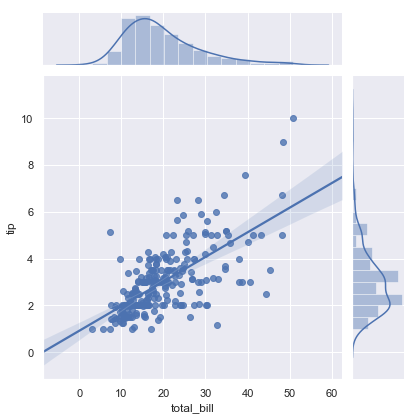
sns.jointplot(x="total_bill", y="tip", data=tips, kind="reg")
结果如下图所示:
用函数pairplot()并用参数”kind=’reg’“结合函数regplot()和PairGrid来展示数据集中变量之间的线性关系。与lmplot()的不同之处是两个轴不显示基于第三个变量的两个level的相同关系;相反pairgrid()用于显示数据集中变量的不同对之间的多个关系。
sns.pairplot(tips, x_vars=["total_bill", "size"], y_vars=["tip"],
height=5, aspect=.8, kind="reg")
结果如下图所示:
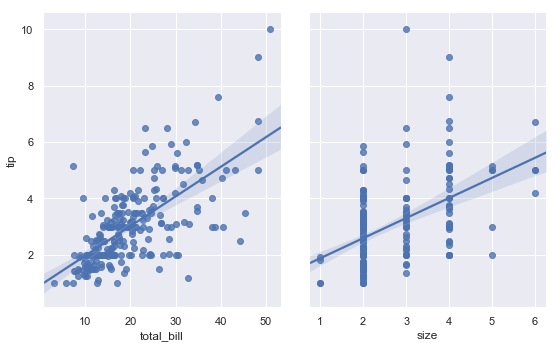
与lmplot()类似,但与jointplot()不同,pairplot()中使用“hue”参数内置了附加分类变量的条件:
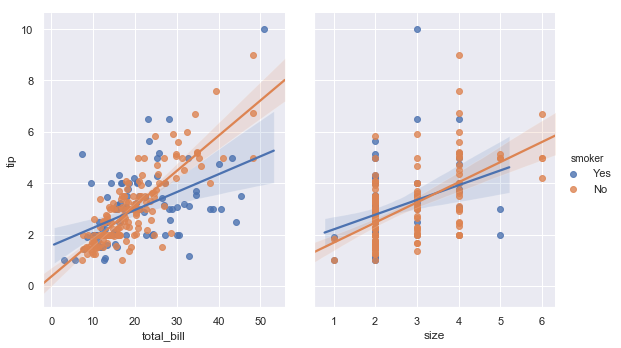
sns.pairplot(tips, x_vars=["total_bill", "size"], y_vars=["tip"],
hue="smoker", height=5, aspect=.8, kind="reg")
结果如下图所示:
参考文献:
http://seaborn.pydata.org/tutorial/regression.html